Comparing Methods for Estimating 95% Confidence Intervals of Proportions: Wald, Wilson, and Equal-Tailed Jeffreys Prior
How much can you trust a number when dealing with rare events?
In statistics, it’s not just about getting an estimate — it’s about knowing how uncertain that estimate really is.
Introduction
Estimating confidence intervals (CIs) for proportions is a fundamental task in statistical analysis, particularly in fields like epidemiology, public health, and rare disease research.
Confidence intervals provide a measure of uncertainty around point estimates like incidence rates, prevalence, and response rates, helping researchers and decision-makers gauge the reliability of their findings.
However, constructing accurate confidence intervals for proportions is not always straightforward—especially when dealing with small sample sizes or rare events, where traditional methods may fall short.
In this post, we focus on three widely used methods for estimating 95% confidence intervals for proportions:
-
Wald Method:
A traditional approach based on the normal approximation, known for its simplicity but prone to inaccuracies in small samples or when proportions are close to 0 or 1.
-
Wilson Method:
An improved frequentist method that adjusts for the shortcomings of Wald, offering more reliable intervals that stay within logical bounds.
-
Equal-Tailed Jeffreys Prior Method:
A Bayesian approach using a non-informative prior, known for its excellent frequentist properties and particularly strong performance in rare event settings.
Through simulations designed to mimic rare disease scenarios, we will benchmark these methods, providing both empirical insights and practical Python code to guide method selection in real-world analyses.
Purpose of the post
Which method gives the most reliable confidence interval for proportions? The short answer: it depends. As highlighted by the classic review by Brown et al., the performance of CI estimation methods can vary based on factors like sample size and how close the true proportion is to 0 or 1.
This post puts three popular methods—Wald, Wilson, and the equal-tailed Jeffreys prior—to the test using simulated data. By benchmarking their performance, especially in rare disease contexts where small samples are common, we aim to provide practical guidance for choosing the right method—along with reusable Python code for each.
Understanding Confidence Intervals for Proportions
In statistical analysis, a confidence interval (CI) provides a range of plausible values for an unknown population parameter based on observed data.
When estimating a proportion—such as the incidence of a rare disease, the prevalence of a microbial species, or a treatment success rate—the confidence interval quantifies the uncertainty around the point estimate.
Rather than relying solely on a single value (e.g., “2% prevalence”), a 95% confidence interval might tell us that the true prevalence is likely between 1.5% and 2.7%, offering a more complete picture of the estimate’s reliability.
Mathematically, a 95% CI means that if we were to repeat the study many times under the same conditions, about 95% of the constructed intervals would contain the true proportion.
Why Accurate Interval Estimation Matters
Accurate estimation of confidence intervals is critically important in fields like epidemiology and microbiome research, where:
-
Rare Disease Studies:
Small sample sizes and extremely low event rates are common. Overly narrow or inaccurate intervals can falsely suggest high precision, leading to misguided conclusions about disease risk, treatment efficacy, or healthcare burden.
-
Microbiome Studies:
The presence or abundance of microbial taxa can be rare or highly variable. Reliable intervals help interpret findings with appropriate caution, avoiding overinterpretation of noisy or sparse data.
Poorly constructed intervals—especially those that underestimate uncertainty—can mislead both researchers and policymakers, leading to flawed decision-making, missed treatment opportunities, or inappropriate resource allocation.
Thus, selecting a method that maintains valid coverage while offering reasonable precision is not merely a technical preference; it is essential for trustworthy science.
Overview of the Methods
Building on insights from Brown et al., here’s a practical overview of the Wald, Wilson, and Jeffreys methods—covering key concepts, formulas, and typical use cases.
Wald Method
-
Formula:
\[\hat{p} \pm z_{\alpha/2} \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}}\] -
Summary:
Simple and widely taught, but often inaccurate—especially with small samples or proportions near 0 or 1.
-
Limitations:
Poor coverage, unstable even with moderate to large samples; not recommended for rare event settings.
Wilson Method
-
Formula:
\[\frac{\hat{p} + \frac{z^2}{2n} \pm z \sqrt{ \frac{\hat{p}(1 - \hat{p})}{n} + \frac{z^2}{4n^2} }}{1 + \frac{z^2}{n}}\] -
Summary:
A corrected method that improves coverage and keeps intervals within [0,1].
-
Advantages:
Reliable even with small samples; recommended for real-world use over Wald.
Jeffreys Method
-
Formula:
Based on Beta posterior:
\[\text{Beta}(X+0.5, n-X+0.5)\] -
Summary:
A Bayesian-based method with strong frequentist performance, especially for rare events.
-
Advantages:
Excellent coverage, stable near boundaries, highly suitable for small sample and rare event studies.
Estimating Confidence Intervals: A Hands-On Example
Before diving into large-scale simulations, let’s first walk through a simple example to see how the three methods—Wald, Wilson, and Jeffreys—work in practice.
We’ll assume:
- Sample size (n): 2000
- Number of cases (x): 1
Using Python’s statsmodels package, we can easily calculate the 95% confidence intervals for the proportion estimate using each method.
from statsmodels.stats.proportion import proportion_confint
import numpy as np
# Set the random seed for reproducibility
np.random.seed(123)
# Define parameters
cases = 1
n = 2000
# 1. Wald method
ci_wald_estimate = proportion_confint(cases, n, alpha=0.05, method='normal')
print(f'95% Wald CI: [{ci_wald_estimate[0]:.4f}, {ci_wald_estimate[1]:.4f}]')
# 2. Wilson method
ci_wilson_estimate = proportion_confint(cases, n, alpha=0.05, method='wilson')
print(f'95% Wilson CI: [{ci_wilson_estimate[0]:.4f}, {ci_wilson_estimate[1]:.4f}]')
# 3. Jeffreys method
ci_jeffreys_estimate = proportion_confint(cases, n, alpha=0.05, method='jeffreys')
print(f'95% Jeffreys CI: [{ci_jeffreys_estimate[0]:.4f}, {ci_jeffreys_estimate[1]:.4f}]')
Output:
95% Wald CI: [0.0000, 0.0015]
95% Wilson CI: [0.0001, 0.0028]
95% Jeffreys CI: [0.0001, 0.0023]
Key Observations
- Wald method technically stays within the [0,1] range, but its lower bound rounds to zero, reflecting how poorly it behaves for very small proportions.
- Wilson method corrects for this issue and offers a wider, safer interval that remains fully positive.
- Jeffreys method also produces a valid and slightly narrower interval compared to Wilson, benefiting from Bayesian adjustments that naturally avoid the zero-boundary problem.
This small example already shows a clear trend: for rare events (like in rare disease epidemiology), robust methods like Wilson and Jeffreys provide more reliable and interpretable intervals than the traditional Wald method.
In the next section, we’ll benchmark these methods more systematically using simulated datasets across a range of sample sizes and true proportions.
Comparing the Methods
To systematically evaluate the performance of the Wald, Wilson, and Jeffreys methods, we conducted a benchmark analysis using simulated data designed to mimic real-world rare disease studies.
We intentionally defined:
- Sample sizes ranging from 30 to 30,000, representing single-center cohorts up to large national registries.
- True event proportions ranging from 0.0005 to 0.02, reflecting the extremely low rates typical in rare diseases.
# Define simulation parameters
sample_sizes = [30, 100, 300, 1000, 30000]
true_proportion = [0.0005, 0.001, 0.005, 0.01, 0.02]
n_simulations = 1000
Performance Metrics
We evaluated each method based on two key metrics:
- Coverage Probability: How often the 95% confidence interval contains the true proportion (i.e., accuracy).
- Average Confidence Interval Width: Reflecting the precision of the estimate (narrower is better, assuming coverage is adequate).
This setup allows us to explore an important practical question:
Which method strikes the best balance between accuracy and precision, especially under challenging rare disease conditions?
Coverage Probability
The figure above shows how the coverage probability varies across different sample sizes and true proportions for the three methods: Wald, Wilson, and Jeffreys. The dashed red line marks the target 95% coverage.
Key Observations:
- Jeffreys Method:
- Jeffreys consistently maintains or exceeds 95% coverage across all combinations of sample sizes and true proportions.
- Even in very small samples (e.g., n=30) and extremely low proportions (e.g., 0.0005), Jeffreys remains robust.
- This highlights its strength for rare event scenarios where maintaining coverage is critical.
- Wilson Method:
- Wilson performs comparably to Jeffreys in many scenarios, particularly as sample size increases.
- However, at very small sample sizes (e.g., n=30, 100) and very rare proportions (e.g., 0.0005–0.001), Wilson coverage sometimes drops slightly below 95%.
- It becomes increasingly reliable as sample size grows.
- Wald Method:
- Wald shows poor coverage in almost all small-to-moderate sample size settings, often falling far below the 95% target.
- At very low true proportions (e.g., 0.005 or lower), even increasing sample size to 1000 does not fully rescue the Wald method.
- Only with very large sample sizes (n=30,000) and higher true proportions (e.g., 0.02) does Wald approach acceptable coverage.
Additional Nuances:
- Effect of True Proportion:
- Lower true proportions (e.g., 0.0005, 0.001) make it harder for methods to maintain ideal coverage, especially noticeable for Wald and, to a lesser extent, Wilson.
- As true proportion increases (e.g., 0.02), all methods tend to perform better, but differences still remain.
- Effect of Sample Size:
- Larger sample sizes systematically improve coverage for all methods, but Wald still lags behind unless the sample size is very large.
Practical Implications:
- Jeffreys method is the most dependable choice for rare event settings where preserving nominal confidence levels is crucial.
- Wilson method is a strong practical alternative, especially in moderate-to-large sample settings, offering better behavior than Wald.
- Wald method should generally be avoided for rare disease applications unless working with extremely large cohorts and relatively higher event proportions.
Average Confidence Interval Width
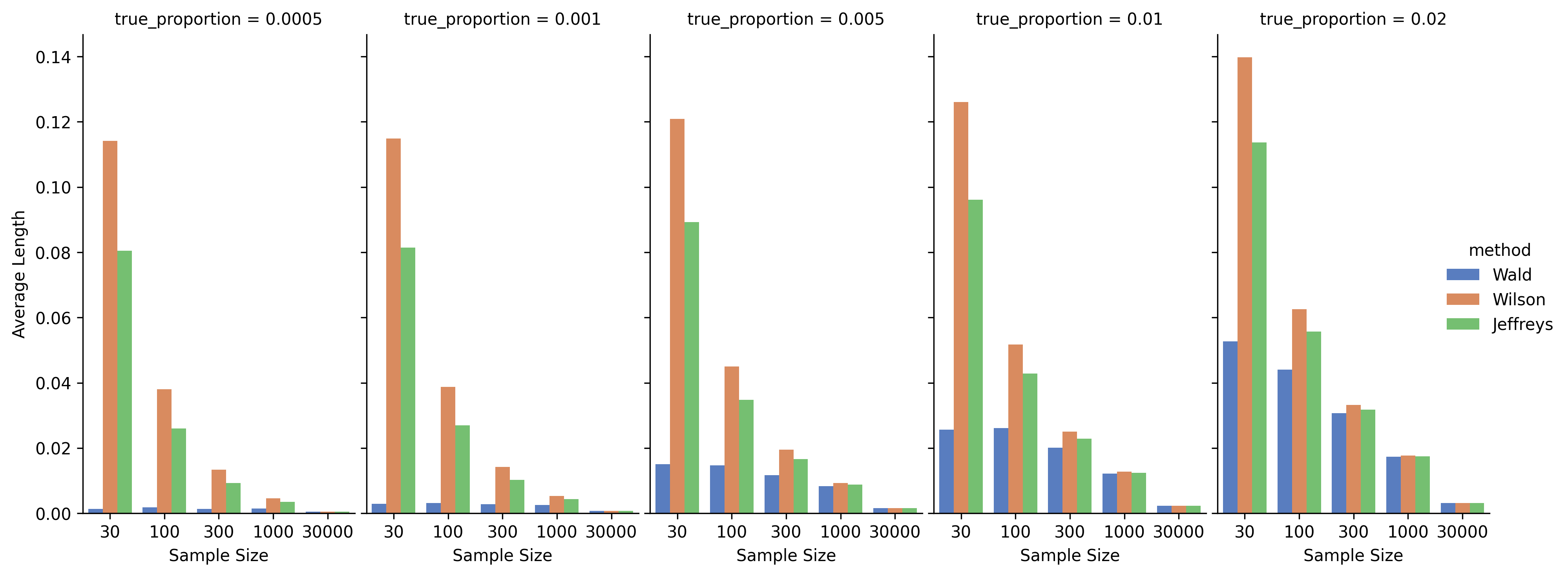
95% CI width by methods controlling for the sample sizes and true proportions
The figure above illustrates the average length of 95% confidence intervals across different sample sizes and true proportions, comparing the Wald, Wilson, and Jeffreys methods.
Key Observations:
- Wald Method:
- Wald consistently produces the narrowest confidence intervals across all settings.
- However, given Wald’s poor coverage performance (as seen in the previous figure), these narrower intervals are misleading — they falsely suggest higher precision while actually underestimating the true uncertainty.
- Thus, the apparent precision of Wald should be interpreted with caution: it’s a false sense of accuracy.
- Wilson and Jeffreys Methods:
- Wilson intervals are wider than Jeffreys across almost all settings, particularly noticeable when both sample size is small and true proportion is low.
- Jeffreys consistently achieves slightly narrower intervals than Wilson while still maintaining better or comparable coverage.
- This suggests Jeffreys method offers superior precision among the reliable methods.
- Effect of Sample Size:
- As sample size increases, the width of the confidence intervals shrinks for all methods, as expected.
- When sample size reaches 30,000, all methods yield very narrow intervals, and differences between methods become minimal.
- Effect of True Proportion:
- Larger true proportions (e.g., 0.02) generally lead to wider intervals compared to extremely low proportions (e.g., 0.0005), because variance is inherently higher when the probability is farther from 0 or 1.
Practical Considerations
When selecting a method to construct confidence intervals for proportions—especially in rare disease contexts—it is crucial to match the method to the study’s characteristics. Below are key guidelines and common pitfalls to watch for:
Choosing the Appropriate Method
| Scenario | Recommended Method | Reason |
|---|---|---|
| Very small sample size (n ≤ 100) and rare events | Jeffreys | Best coverage; robust even with extreme rarity |
| Moderate sample size (n ~ 300–1000), low prevalence | Jeffreys or Wilson | Both offer reliable coverage; Jeffreys slightly narrower intervals |
| Large sample size (n ≥ 10,000), moderate proportions (e.g., 0.01–0.02) | Wilson or Jeffreys | Minor differences; both safe choices |
| Extremely large sample size (n ≥ 30,000) with not-so-rare events | Wilson (or even Wald) | Wald acceptable only under these conditions |
Potential Pitfalls and How to Avoid Them
- Pitfall 1: Blindly Using the Wald Method
- Issue: Wald intervals can be too narrow and may miss the true proportion, especially with small samples or low event rates.
- Solution: Prefer Wilson or Jeffreys methods for rare events or small sample studies.
- Pitfall 2: Overemphasizing Narrow Intervals
- Issue: A narrow interval is meaningless if coverage probability is poor (i.e., interval doesn’t capture the true proportion reliably).
- Solution: Prioritize methods with strong coverage (like Jeffreys and Wilson) before focusing on interval width.
- Pitfall 3: Assuming “One Size Fits All”
- Issue: The best method depends on both sample size and true event rate.
- Solution: Tailor your method choice based on study characteristics (refer to the table above).
Conclusion
Choosing the right method to estimate confidence intervals for proportions is critical—especially when studying rare events in small cohorts, as is often the case in rare disease research.
This analysis highlights that:
- Jeffreys method consistently delivers the best balance: reliable coverage and high precision across challenging scenarios.
- Wilson method remains a strong, practical alternative, particularly when ease of interpretation or computational simplicity is needed.
- Wald method, despite its simplicity, should be avoided unless working with extremely large samples and relatively high event rates.
In rare disease studies where sample sizes are often small and events are extremely rare, robust methods like Jeffreys or Wilson are not just preferable—they are essential for trustworthy statistical inference.
When precision matters, and lives or health policy decisions could depend on these estimates, choose your method thoughtfully.
Good science begins with good measurement.
Putting It Into Practice
To help you apply these methods in your own work, I’ve prepared clean, reusable Python code that:
- Calculates Wald, Wilson, and Jeffreys confidence intervals
- Benchmarks performance across different sample sizes and true proportions
- Summarizes key metrics like coverage probability and interval width
You can easily adapt the code to:
- Analyze your own datasets
- Test other confidence levels (e.g., 90%, 99%)
- Extend the benchmarking to new methods
Whether you’re working on rare disease epidemiology, microbiome studies, or any research involving proportions, these code snippets are ready to plug into your analysis.
Access the full code here.